A substantially updated version of the hypertextbook is available here. Please migrate to that version. This one will eventually disappear.
How fast do solutes diffuse into or out of a biofilm?
We have tools to visualize diffusion in biofilms

Compare this image with the movie on the left, which shows a chemical diffusing into the biofilm.
Image analysis of data from these types of experiments afforded an estimate of the effective diffusion coefficient of Rhodamine B in the biofilm. The average value of De, the effective diffusion coefficient in the biofilm, was 11 percent of its value in water. For details, see Abdul Rani et al. (2005) Antimicrob. Agents Chemother., in press.We can also calculate diffusion times
Suppose a stain is added to the medium bathing a biofilm. How long will it take this dye to permeate, by diffusion, to the interior of a cell cluster or to the bottom of the biofilm? To get started, we will define a single, simple measure of diffusive penetration time. There are two versions of this measure, depending on the geometry of the system. The time required for a solute added to the fluid bathing a biofilm to attain 90% of the bulk fluid concentration at the base of flat slab (uniformly thick) biofilm is given very simply by:
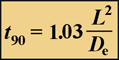 (1)
(1)
Here, L is the biofilm thickness, and Deis the effective diffusion coefficient in the biofilm.
The time required for a solute to attain 90% of the bulk fluid concentration at the center of a spherical biofilm cell cluster is given by:
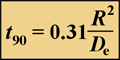 (2)
(2)
where R is the cluster radius and De is the effective diffusion coefficient in the biofilm. The first step in performing these calculations is to estimate the effective diffusion coefficient in biofilm.
Biofilms are mostly water, and the appropriate starting point for estimating a diffusion coefficient in a biofilm is to determine the value of the diffusion coefficient in pure water (Daq. Some aqueous diffusion coefficients have been experimentally measured and can be found in the literature. Others can be estimated from a predictive correlation such as the Wilke-Chang correlation. The single number relevant to biofilms is 2.6, the diffusion coefficient for water.
Aqueous diffusion coefficients of selected solutes of interest in microbial systems are tabulated in Table 4-1. The values of diffusion coefficients in water of various biocides and antibiotics have been summarized elsewhere (32, 34).
Use the scrollbar to read this table, or View Table 1 in full window.
The diffusion coefficient in water depends on temperature, both directly and through the effect of temperature (T) on the solution viscosity (µ). This temperature dependence of aqueous diffusion coefficients can be calculated through the relationship Daqµ/T = constant.
Use the scrollbar to read this table, or View Table 2 in full window.
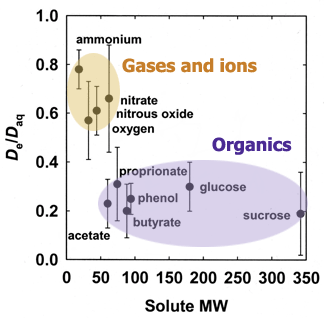
The value of the effective diffusion coefficient in the biofilm will be reduced compared to the diffusion coefficient in water due to the presence of microbial cells, extracellular polymers, and abiotic particles or gas bubbles that are trapped in the biofilm. This reduction is described by the ratio De/Daq. Experimental measurements of this ratio, termed the relative effective diffusivity, have been reviewed elsewhere (33) and that article presents guidelines and formulae for estimating De/Daq in biofilms. There are also sophisticated approaches for calculating this ratio (40). The relative effective diffusivity depends on the biomass density in the biofilm and the physiochemical properties of the solute. De/Daq in biofilm ranges from ca. 0.2 to 0.8 with a mean value of ca. 0.4. The figure below presents consensus values of De/Daq for selected solutes. A value for De/Daq of 0.6 is suggested for small inorganic ions and light gases (e.g., oxygen, nitrous oxide, carbon dioxide, or methane), and a value for De/Daq of 0.25 is suggested for most organic solutes.
Four example calculations
Armed with an effective diffusion coefficient and an estimate of the biofilm thickness or cluster radius, the calculation of diffusive penetration times is straightforward. The best way to illustrate this is with some example calculations.
Example calculation 4-1 is presented below in both text and as a narrated slide show. Prepared and narrated by Dr. Philip Stewart, Professor of Chemical and Biological Engineering at Montana State University, Bozeman, Montana
Example calculation 4-1: Text version
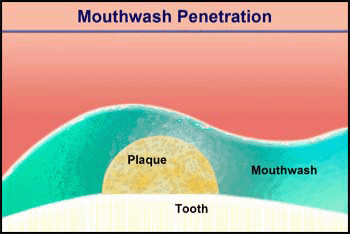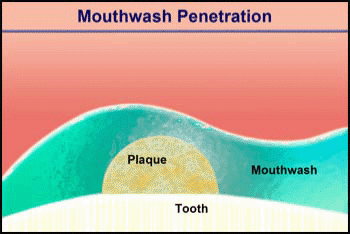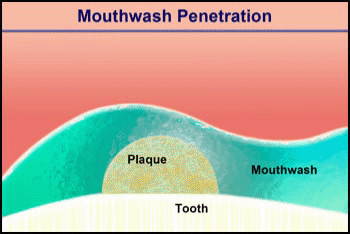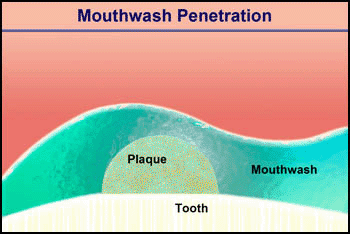
Consider the penetration of a mouthwash into a roughly hemispherical patch of dental plaque with a radius of 280 µm. How long must one rinse with a mouthwash containing chlorhexidine to have this antimicrobial agent penetrate down to the tooth surface underneath the center of the plaque? The diffusion coefficient of chlorhexidine in water, as estimated by the Wilke-Chang correlation, is 3.7 x 10-6 cm2 s-1 (34). Holding the mouthwash in the mouth will raise its temperature; assume that the mean temperature is 30°C. The aqueous diffusion coefficient at 30°C is then 4.2 x 10-6 cm2 s-1. From Stewart (33) the value of De/Daq in dental plaque for a solute such as chlorhexidine is predicted to be ca. 0.2. This gives a value of De of 0.84 x 10-6 cm2-s. Using the formula for a sphere (0.31 R2/De), which also applies to a hemisphere on an impermeable plane, the diffusion time is calculated to be 289 s. Try swishing mouthwash for this period to develop a new appreciation for just how long five minutes is.
Now you try it. . .
A researcher plans to test the role of a homoserine lactone (HSL) quorum sensing signal on biofilm phenotypes by adding exogenous HSL to the bulk fluid. If the biofilm is treated as a flat slab that is 80 microns thick, estimate the time needed for N-(3-oxododecanoyl)-L-homoserine lactone to reach 90 percent of its bulk fluid concentration at the base of a biofilm. The temperature is 25oC.
Resources:
Equation 4-1: Calculating diffusion time in a flat slab biofilm
View Table 4-1: Diffusion coefficients in water at 25°C
View Table 4-2: Temperature dependence of aqueous diffusion coefficients
Calculator for Equation 4-1
I'd like some HELP.
I'd Like some HELP.
I'd like some Help.
Which is the correct answer?:
- 14 s
- 54 s
- 80 s
- 327 s
Example calculation 4-2
A biofilm growing in a flow cell at room temperature (22°C) is to be stained with a fluorescein-tagged probe. The biofilm consists of tightly packed mushroom-shaped clusters that are 100 µm tall. How long must the sample be incubated with this reagent to ensure that the stain reaches to the full depth of the biofilm? Suppose that the diffusion coefficient of the fluorescent probe in water is half that of fluorescein, or 2.7 x 10-6 cm2 s-1 at 25°C. At 22°C this value becomes 2.5 x 10-6 cm2 s-1. Lacking specific information about the biofilm, we can take De/Daq to be 0.25. This gives a value of De of 0.63 x 10-6 cm2 s-1. Though the biofilm is not uniformly thick, you can treat it as if it were. The result will be a conservative estimate of the required staining time. The diffusion time is 1.03 L2/De, which equals 165 s. Staining for a few minutes should suffice.
Example calculation 4-3
A mixed-species biofilm grown for 6 days is 1,000 µm thick and locally uniform in thickness. Sodium chloride is added to the bulk fluid, and the appearance of the chloride ion is detected by using a microelectrode positioned near the substratum at the base of the biofilm. Estimate how long it takes for the chloride concentration at the substratum to reach 90% of the bulk fluid concentration. The system temperature is 24°C. The diffusion coefficient of chloride ion in water at 24°C is 20 x 10-6 cm2 s-1. Taking De/Daq to be 0.70, De is 14 x 10-6 cm2 s-1. The required penetration time is 714 s or almost 12 min. This calculation is based on an experiment reported by Stewart et al. (35), and the calculated time scale is in rough agreement with the experimental result (1,000 s).
Example calculation 4-4
An experimenter proposes to test the role of a certain gene in biofilm development by overexpressing the gene at a particular stage in the maturation of the biofilm. The gene is placed under the control of a promoter that can be induced by adding IPTG (isopropyl-ß-D-thiogalactopyranoside). This inducer will be added when young microcolonies are forming. These microcolonies can be approximated as hemispherical patches of radius 5 µm. It is desired to calculate any delay in gene expression that might result from the time needed for the IPTG to diffuse throughout the nascent colony. The system temperature is 37°C. IPTG is a modified monosaccharide, so we can estimate that its diffusion coefficient in water at 25°C will be ca. 6.5 x 10-6 cm2 s-1. Scaling to 37°C and taking De/Daq to be 0.25, De is found to be 2.2 x 10-6 cm2 s-1. The required penetration time is a mere 0.12 s. The delay anticipated for diffusive ingress is negligible.
Four assumptions implicit in these calculations
Having made these calculations, it is now appropriate to disclose the four assumptions implicit in them. Two of the assumptions are particularly critical because they are often invalid. The first of these is that resistance to mass transfer outside of the biofilm can be neglected. In plain language, this means that the concentration of the diffusing solute right at the biofilm surface is essentially the same as its concentration in the well-mixed bulk fluid. The other key assumption is that the solute whose penetration is being analyzed does not sorb or react in the biofilm. Both assumptions, if violated, will cause the actual penetration time to be longer than the calculated time. The preceding calculations, therefore, are best regarded as lower bounds on the actual diffusion time.These two issues are discussed at greater length in the following paragraphs. The derivation of Equations 4-1 and 4-2 also assumes an impermeable substratum and a uniform effective diffusivity within the biofilm.
The term external mass transfer resistance refers to the barrier to diffusion posed by slow-moving fluid adjacent to a biofilm. The fluid may be moving, but its direction of flow is generally parallel to the biofilm surface when very close to the biofilm. This means that although there is convective transport in the direction of flow, there is little or no convection in a direction that would carry a solute into or out of a cell cluster. The extent of external mass transfer resistance depends on the hydrodynamics of the system. There is probably little external mass transfer resistance in high-velocity, turbulent flows. External mass transfer resistance is likely important in many laminar flow systems and is assuredly an issue in systems in which the fluid is static. There are quantitative approaches to calculating the effects of external resistance, but these are beyond the scope of this chapter. Suffice it to say that all of the diffusion-related phenomena discussed in this article will only be exacerbated when external mass transfer resistance is present.
Penetration times calculated by using Equation 4-1 or 4-2 will be reasonable estimates as long as there is no significant reaction or sorption of the solute in the biofilm. It may be easiest to appreciate this caveat by considering a couple of examples in which these equations break down. The diffusive penetration of IPTG calculated in the last example above depends on there being no metabolism of this molecule. While sugars have diffusion coefficients in water that are similar to that of IPTG, it would be incorrect to apply the IPTG result to the transport of a sugar if the microorganisms are capable of metabolizing that saccharide. Microbial utilization of the sugar will reduce its concentration as it diffuses into the biofilm. It would also be incorrect, for example, to equate the penetration time for the chloride ion (Cl-) calculated in the third example above with the penetration time for the hypochlorite ion (OCl-), even though these two ions have essentially the same diffusion coefficient in water. Whereas the chloride ion is inert, the hypochlorite ion is highly reactive and will be neutralized by reactions with organic matter in the biofilm. These reactions profoundly retard penetration of this species (6, 35). When a solute reacts in the biofilm it may never fully penetrate the biofilm. Reaction and diffusion achieve a steady balance that leads to persistent concentration profiles within the biofilm. This interaction is the subject of the next section.